CS641 Class 7 Sec 2.4, 2.5
Section 2.4: Signed and
Unsigned Numbers
Review of 2s complement.
Last time used the fact that -1 = 1111...1111, and noted that adding one to it rolled everything over to result in 0.
Subtracting one yields 1111....1110, and that’s -2, and so on until the most negative number, 1000....0000
Adding one to 0 yields 000...0001, ... 0111...11111, most positive number.
All negative numbers have bit 31 = 1
This is talking about signed numbers. C and Java int, C long long and Java long
Unsigned Numbers
C, but not Java, also supports an unsigned number type.
Same add-one operation, but different interpretation of value:
0 = 000...000
1 = 000...001
...
max = 111...111 about twice as big as max signed
No “sign bit”, just another data bit.
So unsigned int x; can hold numbers from 0 up to 4G-1
But don’t be enticed into using unsigned ints just for that extra bit! Use long longs and stay signed, for understandable code.
What is a legitimate use for unsigned int type? Address values, though we usually use these inside pointers, which have a more descriptive type.
One might think that array subscripts should be unsigned, but this is hardly ever done.
Little numbers, squeezed into a few bits, are often unsigned
Best to avoid unsigned type in C in new code.
Instructions as Numbers
° One word is 32 bits, so divide instruction word into “fields”.
° Each field tells computer something about instruction.
° We could define different fields for each instruction, but MIPS is based on simplicity, so define 3 basic types of instruction formats:
• R-format
• I-format
• J-format
° I-format: used for instructions with immediates, lw and sw (since the offset counts as an immediate), and the branches (beq and bne),
• (but not the shift instructions; later)
° J-format: used for j and jal
° R-format: used for all other instructions
° It will soon become clear why the instructions have been partitioned in this way.
R-Format Instructions
° Define “fields” of the following number of bits each: 6 + 5 + 5 + 5 + 5 + 6 = 32
![]()
![]()
° Important: On these slides and in book, each field is viewed as a 5- or 6-bit unsigned integer.
• Consequence: 5-bit fields can represent any number 0-31, while 6-bit fields can represent any number 0-63.
° opcode: partially specifies what instruction it is Note: This number is equal to 0 for all R-Format instructions.
° funct: combined with opcode, this number exactly specifies the instruction
° rs (Source Register, 5 bits): generally used to specify register containing first operand
° rt (Target Register, 5 bits): generally used to specify register containing second operand (note that name is misleading)
° rd (Destination Register, 5 bits): generally used to specify register which will receive result of computation
°
shamt
(5 bits): This field contains the amount a shift instruction will shift
by. Shifting a 32-bit word by more than
31 is useless, so this field is only 5 bits (so it can represent the numbers
0-31). This field is set to 0 in all but the shift instructions.
R-Format Example
add $8,$9,$10
opcode = 0 (look up in table in book)
funct = 32 (look up in table in book)
rs = 9 (first operand)
rt = 10 (second operand)
rd = 8 (destination)
shamt = 0 (not a shift)
Called a Machine Language Instruction:
![]()
![]()
![]()
hex representation: 012A 4020hex
I-Format Instructions
° What about instructions with immediates?
• 5-bit field only represents numbers up to the value 31: immediates may be much larger than this
• Ideally, MIPS would have only one instruction format (for simplicity): unfortunately, we need to compromise
° Define new instruction format (I-format) that is partially consistent with R-format:
• First notice that, if instruction has immediate, then it uses at most 2 registers.

• opcode: same as before except that, since there’s no funct field, opcode uniquely specifies an instruction in I-format
• This also answers question of why R-format has two 6-bit fields to identify instruction instead of a single 12-bit field: in order to be consistent with other formats.
• rs: specifies the only register operand (if there is one)
• rt: specifies register which will receive result of computation (this is why it’s called the target register “rt”)
• The Immediate Field:
• addi, slti, sltiu, the immediate is sign-extended to 32 bits. Thus, it’s treated as a signed integer.
• Ori , the immediate is not sign-extended
• 16 bits è can be used to represent immediate up to 216 different values
• This is large enough to handle the offset in a typical lw or sw, plus a vast majority of values that will be used in the slti instruction.
I-Format Example
addi $21,$22,-50
opcode = 8 (look up in table in book)
rs = 22 (register containing operand)
rt = 21 (target register)
immediate = -50 (by default, this is decimal)

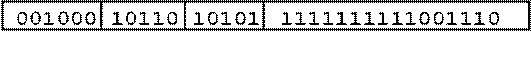
hexadecimal
representation: 22D5 FFCEhex
Recall that 32 bit immediates (constants) are also needed, and loaded with help from lui instruction.
Branches: PC-Relative Addressing
° Use I-Format

° rs and rt specify registers to compare
° What can immediate specify?
• Immediate is only 16 bits
•
PC (Program Counter) has byte address of
current instruction being executed;
32-bit pointer to memory
• So immediate cannot specify entire address to branch to.
• may want to branch to anywhere in memory, but a branch often changes PC by a small amount
• Solution to branches in a 32-bit instruction: PC-Relative Addressing
• Let the 16-bit immediate field be a signed two’s complement integer to be added to the PC if we take the branch.
• Now we can branch +/- 215 bytes from the PC, which should be enough to cover almost any loop.
• Any ideas to further optimize this?
• Note: Instructions are words, so they’re word aligned (byte address is always a multiple of 4, which means it ends with 00 in binary).
• So the number of bytes to add to the PC will always be a multiple of 4.
• So specify the immediate in words.
• Now, we can branch +/- 215 words from the PC (or +/- 217 bytes), so we can handle loops 4 times as large.
• Branch Calculation:
• If we don’t take the branch:
• PC = PC + 4
• PC+4 = byte address of next instruction
• If we do take the branch:
• PC = (PC + 4) + (immediate * 4)
• Observations
° Immediate field specifies the number of words to jump, which is simply the number of instructions to jump.
° Immediate field can be positive or negative.
° Due to hardware, add immediate to (PC+4), not to PC; will be clearer why later in course
MIPS Code:
Loop: beq $9,$0,End
add $8,$8,$10
addi $9,$9,-1
j Loop
End:
beq branch is I-Format:
opcode = 4 (look up in table)
rs = 9 (first operand)
rt = 0 (second operand)
immediate = ???
• Immediate Field:
• Number of instructions to add to (or subtract from) the PC, starting at the instruction following the branch.
• In beq case, immediate = 3


J-Format Instructions: for jumping
further
° For branches, we assumed that we won’t want to branch too far, so we can specify change in PC.
° For general jumps (j and jal), we may jump to anywhere in memory.
° Ideally, we could specify a 32-bit memory address to jump to.
° Unfortunately, we can’t fit both a 6-bit opcode and a 32-bit address into a single 32-bit word, so we compromise.
°
°
![]()
°
![]()
° Keep opcode field identical to R-format and I-format for consistency.
° Combine all other fields to make room for large target address.
° Note that, just like with branches, jumps will only jump to word aligned addresses, so last two bits are always 00 (in binary).
° So let’s just take this for granted and not even specify them.
° Now specify 28 bits of a 32-bit address
° Where do we get the other 4 bits?
° By definition, take the 4 highest order bits from the PC.
° Technically, this means that we cannot jump to anywhere in memory, but it’s adequate 99.9999…% of the time, since programs aren’t that long
° only if straddle a 256 MB boundary
° If we absolutely need to specify a 32-bit address, we can always put it in a register and use the jr instruction.
° Summary:
° New PC = { PC+4[31..28], address, 2’b0 } from green card in book
° Understand where each part came from!
°
Note: { , , } means concatenation
{ 4 bits , 26 bits , 2 bits } = 32 bit address
° { 1010, 11111111111111111111111111, 00 } = 10101111111111111111111111111100
°
We worked out the bit patterns for the “j loop” in the example above:
°
if loop = 0x400000: this is in the first 256M (0x400000 = 4M), so
the top four bits of the PC are 0000, and the bottom 28 bits of the address are
0x400000, and the opcode is 2 (p. B-63). We drop the bottom 2 bits of the address,
leaving 0x1000000:
°
| 2 | 0x1000000|
instruction format
°
new PC = 0|0x100000<<2 = 0x400000
°
If loop = 0x4000 0000, then we’re no longer
in the bottom 256M, ant the top four bits of the PC are 4. The bottom 28 bits
of the address are 0, so we have
°
|2| 0| instruction format
°
new PC = 4|0<<2 = 0x4000 0000