IT 441: Network Services Administration

IT 441: Network Services Administration
Class #05 Exercise

Complete by: 2/22/2018

Log in to users.cs.umb.edu
Log in to a Windows machine
Enter your Unix username as the account name. Then enter your password.

Run the ssh client
Use the values in the table below to connect to users.

ssh configuration parameter value

protocol ssh

ssh version 2

ssh port 22

host users.cs.umb.edu

user name your unix username

Authentication method password

Enter your password
A dialog box will appear on the screen into which you must type the password for your Unix account.
Make sure you are in your home directory
                cd
Go to your it441 directory
                cd  it441
Go to your ex directory
                cd  ex
Create an ex05 directory
                mkdir  ex05
Go to your ex05 directory
                cd  ex05
No need to start up a script session yet...
Create the Perl script positive_negative_zero.pl
#! /usr/bin/perl -lw

...
Make the Perl script executable
chmod +x ./positive_negative_zero.pl
On being run, it should...

Ask the user for a number and store it in a variable

Determine whether the number is positive, negative, or zero.

Output the answer
Create the Perl script verify_even.pl
#! /usr/bin/perl -lw

...
Make the Perl script executable
chmod +x ./verify_even.pl
On being run, it should...

Ask the user for an even number and store the entered value in a variable

If the number is not even, prompt the

Output the number.
Create the Perl script simple_quadratic.pl
#! /usr/bin/perl -lw

...
Make the Perl script executable
chmod +x ./simple_quadratic.pl
We want to write and test a program for solving a quadratic equation of the form:

A*x² + B*x + C = 0

A is the coefficient of x²
B is the coefficient of x
C is the constant
Based on the input, use the quadratic formula to calculate and output the two roots.
x = (-B + square root (B² – 4*A*C))/2*A
On being run, it should...

Prompt the user for coefficient A and store it in a variable.

Prompt the user for coefficient B and store it in a variable.

Prompt the user for coefficient C and store it in a variable.

Using those coefficients, calculate both roots and store each in a separate variable.
(At this point, depending upon the given values of A, B, and C, the code may encounter an error situation and therefore crash. This is okay!)

Output the two roots.

While testing, run a few times trying out different combinations of A, B, and C. In the file, make some comments, noting the different results you get from various combinations. Here are some sample outputs...
Quadratic equation with two real roots
            Enter the coefficient of x squared: -2
            Enter the coefficient of x: 3
            Enter the constant: 4

            Root #1: -0.8507810593582121
            Root #2: 2.350781059358212
Quadratic equation with one real root
            Enter the coefficient of x squared: 2
            Enter the coefficient of x: -12
            Enter the constant: 18

            Root #1: 3.0
            Root #2: 3.0
Quadratic equation with no real roots
(That is, its roots are not within the set of real numbers.)
            Enter the coefficient of x squared: 3
            Enter the coefficient of x: 2
            Enter the constant: 7
            Can't take sqrt of -80 at -e line 1, <> line 3.
(The code fails and you get an error message because it cannot handle that input...)
To check your program against other inputs, look for an online "quadratic equation calculator" like the following: Link
Make a copy of simple_quadratic.pl and call it smart_quadratic.pl
                cp simple_quadratic.pl smart_quadratic.pl
Make sure the copy is executable
ls -l ./smart_quadratic.pl
If it is not executable, then make it so using the chmod utility as in the cases above. Edit smart_quadratic.pl to create a "smarter" version of the previous script, one that can gracefully handle ANY combination of numbers A, B, and C. (This is going to be a conditional, branching problem!)
#! /usr/bin/perl -lw

...
Here are some test values you can use to be sure that your code is giving the correct responses:

Value
for A Value
for B Value
for C Solutions for some possible test cases

1 0 -3 Root #1: 1.7320508075688772
Root #2: -1.7320508075688772

1 1 1 Root #1: -0.5 + i * 0.8660254037844386
Root #2: -0.5 - i * 0.8660254037844386

1 2 1 The only root is -1.0

0 2 4 The only root is -2.0

0 0 6 No value for x is a solution

0 0 0 Any value for x is a solution

Come up with some values of your own to test, as well.
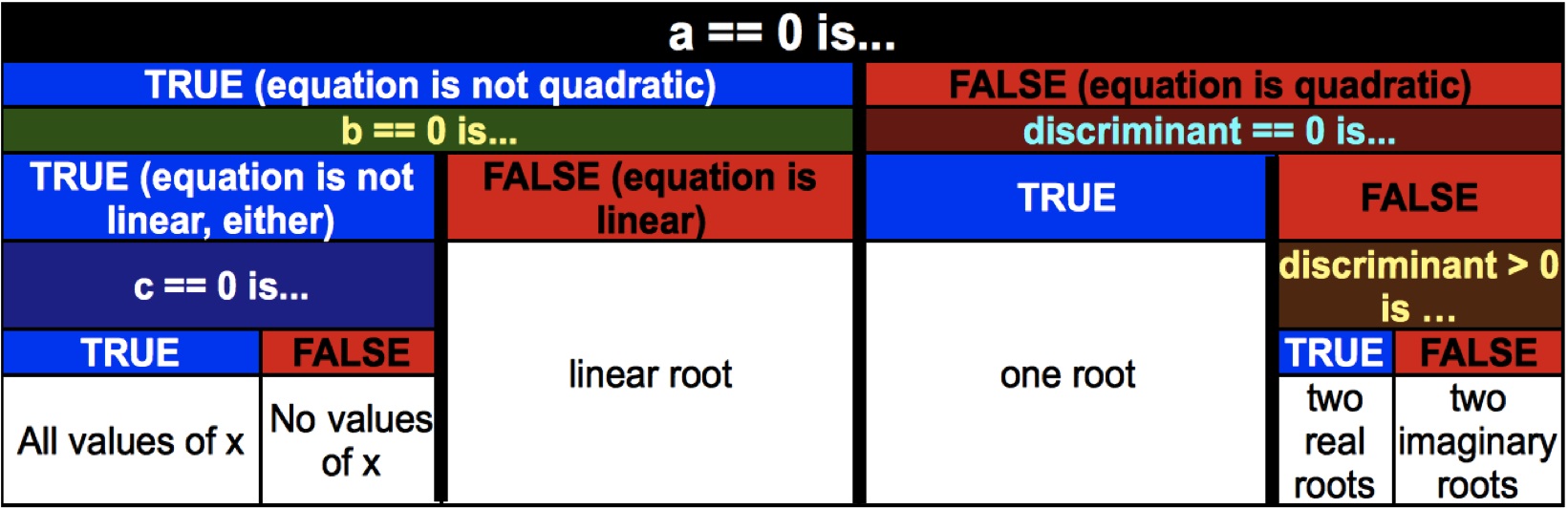
You may be tempted to use a solution of the form if...elsif...else , but I would advise against it. A solution with true branching would be much better because it helps you with "thinking like a computer." Here is a description of the computational logic, in the table below:
Begin a script session
        script
Do a long listing of your ex05 directory -- to confirm your .pl files are all executable
        ls -l
Show and run positive_negative_zero.pl
$ cat ./positive_negative_zero.pl

$ ./positive_negative_zero.pl
(Run the script a few times with different inputs, to confirm correct behavior.)
Show and run verify_even.pl
$ cat ./verify_even.pl

$ ./verify_even.pl
(Run the script a few times with different inputs, to confirm correct behavior.)
Show and run simple_quadratic.pl
$ cat ./simple_quadratic.pl

$ ./simple_quadratic.pl
(Run the script a few times with different inputs, to confirm which coefficient combinations do and do not work.)
Show and run smart_quadratic.pl
$ cat ./smart_quadratic.pl

$ ./smart_quadratic.pl
(Run the script at least six times, using each of six different possible coefficient combinations, using numbers other than those I provided in the table above...

A combination evaluating to two real roots

A combination evaluating to two complex roots

A combination evaluating to one real root

Where A = 0, but B and C are non-zero.

Where A and B are zero, but C is non-zero.

Where all three coefficients are zero.

...to confirm correct behavior.)
End the script session

Use the exit command. You should then have a file called typescript in your current working directory.

ssh configuration parameter	value
protocol	ssh
ssh version	2
ssh port	22
host	users.cs.umb.edu
user name	your unix username
Authentication method	password

Value for A	Value for B	Value for C	Solutions for some possible test cases
1	0	-3	Root #1: 1.7320508075688772 Root #2: -1.7320508075688772
1	1	1	Root #1: -0.5 + i * 0.8660254037844386 Root #2: -0.5 - i * 0.8660254037844386
1	2	1	The only root is -1.0
0	2	4	The only root is -2.0
0	0	6	No value for x is a solution
0	0	0	Any value for x is a solution

IT 441: Network Services Administration Class #05 Exercise Complete by: 2/22/2018

Log in to users.cs.umb.edu

Quadratic equation with two real roots

Quadratic equation with one real root

Quadratic equation with no real roots

Begin a script session

Do a long listing of your ex05 directory -- to confirm your .pl files are all executable

Show and run positive_negative_zero.pl

Show and run verify_even.pl

Show and run simple_quadratic.pl

Show and run smart_quadratic.pl

End the script session

IT 441: Network Services Administration
Class #05 Exercise

Complete by: 2/22/2018