I hope some of the questions are easy. I suggest you do those first. Some are open ended - use your time wisely.

1. Draw n straight lines at random in the plane. "At random" means no two lines are parallel, and no three lines go through a single point. That's sometimes called "general position". These configurations have regions, vertices (where lines intersect) and edges. They're not quite the planar graphs we've studied, since some of the edges have just one vertex and "go off to infinity". Some of the regions do too.

   Here's a picture for n = 4.

   

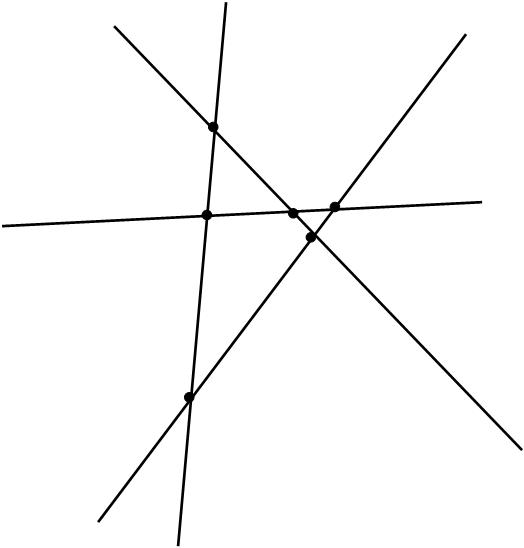
   The following table enumerates some features for n = 2,3 and 4.

                           number of
           lines   vertices  regions   edges  
             2         1        4        4      
             3         3        7        9      
             4         6       11       16      
   

   1. Guess (and prove) the counts for n lines.

   2. Is there an Euler-like formula for these configurations? If so, prove it.

   3. How many colors does it take to color the regions? (Proof, please.)

   4. Can you count the unbounded regions?

   5. Anything else interesting?

2. Let

   	f(x,y,z) = (x + 3y + 5z)2008
   

   1. How many terms (expressions of the form dxaybzc) will there be if you multiply this out?

   2. What is the coefficient of the term x2005y2z1?

   3. We've assumed (without stating it) that when you multiply out the expression the formal variables commute: xy = yx. What is the answer to part (a) if x, y and z represent matrices, for which multiplication may not be commutative.

   Here are some hints you shouldn't need - but I really want to read correct answers, so I'll provide them anyway. (If you didn't need them, let me know. If they helped, let me know that too.)

   • Try out whatever methods you use for the exponents 1 and 2 and perhaps 3 as well before you commit to answers for 2008.
   • We studied a problem like this in class. Remember apples, bananas and cherries?

3. Consider a game of Nim with 2008 piles, containing 1, 2, 4, ..., 2²⁰⁰⁷ chips.

   1. How many chips are there altogether?

   2. What is the Sprague-Grundy value for the starting position?

   3. What first move would you make in this game?

4. Carefully state three definitions or theorems from this course that come with Leonhard Euler's name attached.

5. Find the greatest common divisor of 2008 and 4267 and write it as an integral linear combination of those two numbers.

6. How many integers between 1 and 2008 are relatively prime to 2008?

7. Let t(n) be the number of positive divisors of the integer n. For example, the divisors of 6 are 1, 2, 3 and 6 so t(6) = 4. t(n) = 2 if and only if n is prime.

   1. Complete the following statement and then prove it:

      	t(n) is odd if and only if ...
      

   2. Prove or disprove:

      	 If m and n are relatively prime then t(mn) = t(m)t(n). 
      

   3. Compute t(2008).

8. If there's something in the course you're particularly fond of or spent lots of time studying that I didn't ask about, make up a question here and answer it.