Homework 8
Last updated: Thu, 6 Apr 2023 23:18:05 -0400
Out: Wed Apr 05, 00:00 EST Due: Tue Apr 11, 23:59 EST
This assignment explores decidability and deciders.
Homework Problems
A Decidable Language (12 points)
A Language of DFAs (12 points)
Regular Languages vs Decidable Languages (8 + 8 = 16 points)
Computing Chomsky Normal Form (9 points)
README (1 point)
Total: 50 points
Submitting
Submit your solution to this assignment in Gradescope hw8. Please assign each page to the correct problem and make sure your solutions are legible.
A submission must also include a README containing the required information.
1 A Decidable Language
Prove that the following language is a decidable language:
L_{01} = \{w\mid w\textrm{ is a string where any two consecutive characters are different}\}
Update: You may assume that strings in the language are drawn from alphabet \{\texttt{0},\texttt{1}\}.
If your answer involves a decider, remember that a decider must be accompanied by a termination argument.
That decider must use at least one machine we have previously defined in lecture or homework. Remember that when creating new Turing machines, all other machines or algorithms previously constructed in class or in previous homeworks are available as a "library".
Finally, make sure your decider has an explicit example table that has a separate column indicating whether strings are in the language, and whether strings are accepted by the decider.
2 A Language of DFAs
Prove that the following language is a decidable language:
\textrm{DIFF}_{\textsf{DFA}} = \left\{\left\langle D\right\rangle\mid D\textrm{ is a DFA that accepts all strings where any two consecutive characters are different}\right\}
If your answer involves a decider, remember that a decider must be accompanied by a termination argument.
That decider must use at least one machine we have previously defined in lecture or homework. Remember that when creating new Turing machines, all other machines or algorithms previously constructed in class or in previous homeworks are available as a "library".
Finally, make sure your decider has an explicit example table that has a separate column indicating whether strings are in the language, and whether strings are accepted by the decider.
3 Regular Languages vs Decidable Languages
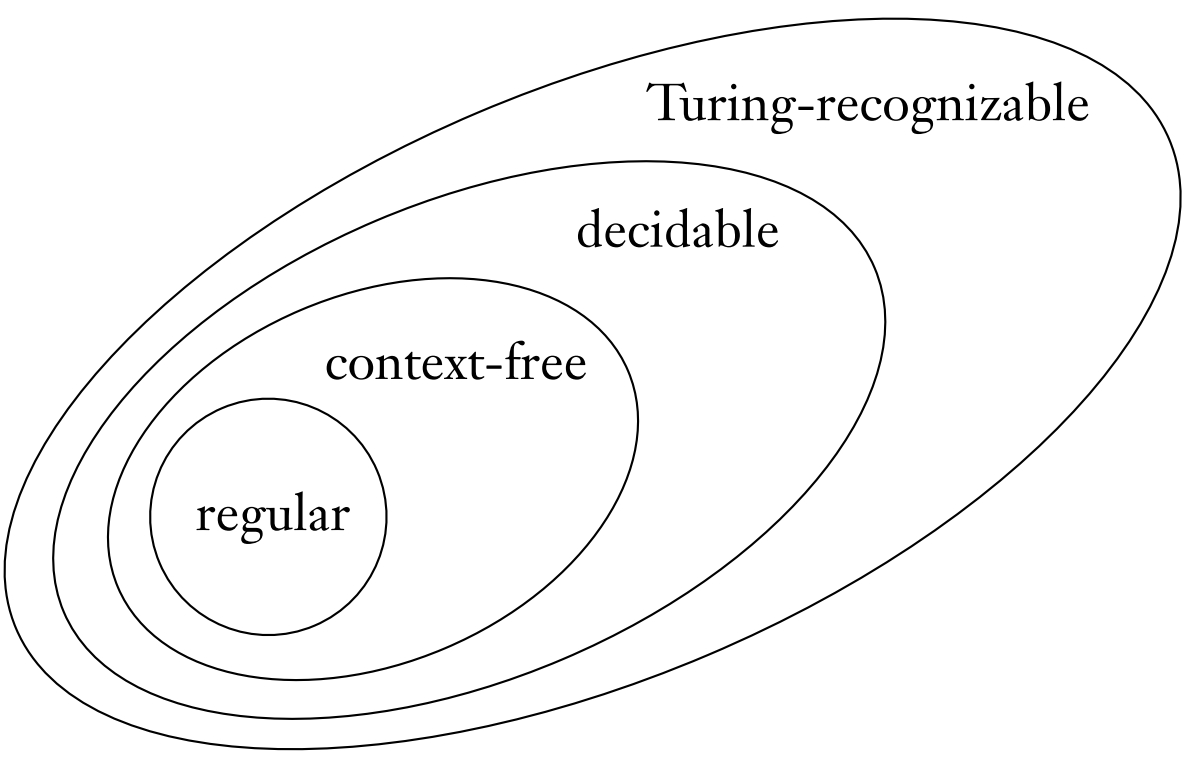
Prove that the "regular" and "decidable" ovals in the language Venn Diagram from class are "correct" with respect to each other.
The "decidable" oval is bigger than the "regular" one.
The "regular" oval is completely inside the "decidable" one.
Give the formal statement to prove.
Prove the formal statement.
4 Computing Chomsky Normal Form
Recall that a CFG is in Chomsky Normal Form (CNF) if all rules have the form:
A \rightarrow BC |
A \rightarrow \texttt{x} |
where \texttt{x} is any terminal, A, B, C are any variables, except B and C are not the start variable.
In addition, a grammar in CNF may include a rule S\rightarrow \varepsilon, where S is the start variable.
Convert the following context-free grammar to Chomsky Normal Form using the algorithm described in class.
S\rightarrow \texttt{a} S \texttt{b}
S\rightarrow SS
S\rightarrow \varepsilon
The start variable of the CFG is S and the set of terminals is \{\texttt{a},\texttt{b}\}