Homework 6

Last updated: Mon, 25 Mar 2024 11:42:52 -0400

Out: Mon Mar 25, 12:00pm EST (noon) Due: Mon Apr 01, 12:00pm EST (noon)

This assignment continues to explore context-free languages (CFLs).

Homework Problems

1. Pushdown Automata (PDAs) (12 points)

2. Regular Language Machine vs CFL Machine (12 points)

3. A Regular Language is Context-Free (12 points)

4. Whitespace Checking is Context-Free? (11 points)

5. README (1 point)

Total: 48 points

Submitting

Submit your solution to this assignment in Gradescope hw6. Please assign each page to the correct problem and make sure your solutions are legible.

A submission must also include a README containing the required information.

1 Pushdown Automata (PDAs)

For the following PDA state diagram:

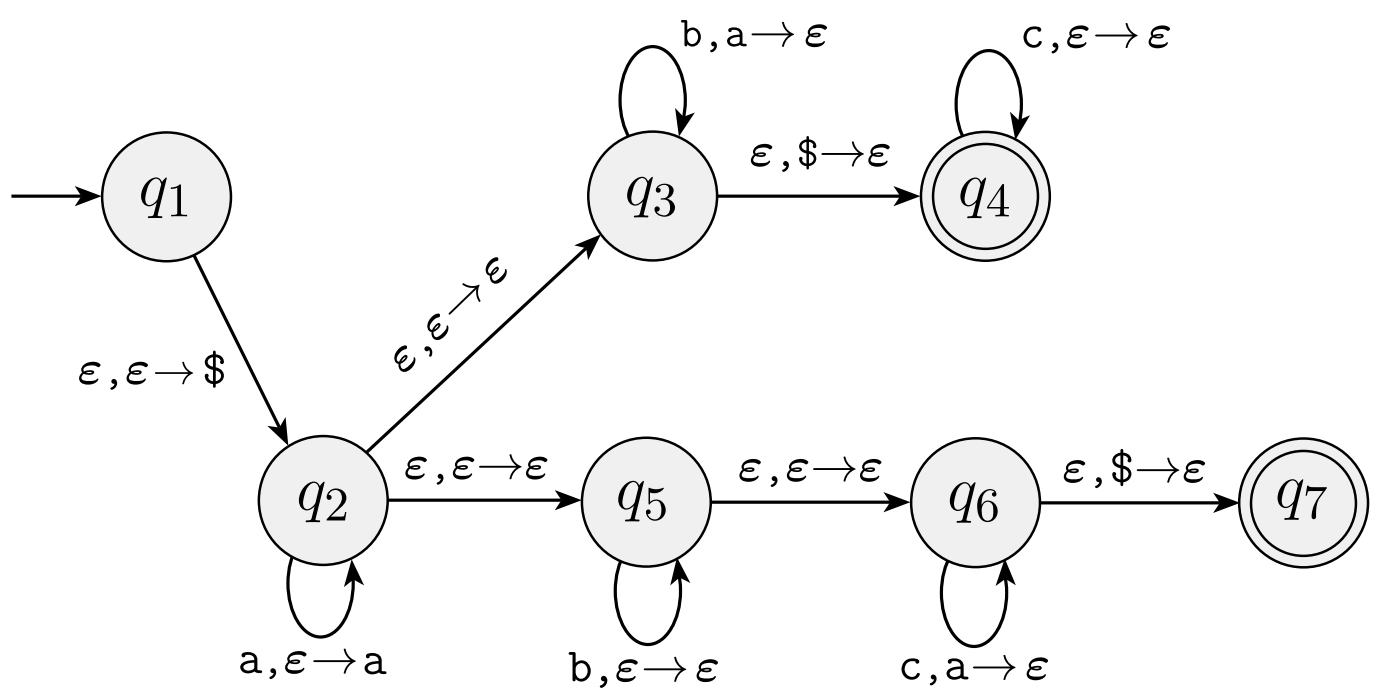
1. Give a formal description of this PDA. Make sure to include all the necessary components.

2. Give two strings that are in the language recognized by this PDA. For each of these strings, give a sequence of configurations that represents an accepting computation for the PDA. One should end in state q_4 and the other in state q_7.

3. Give two strings that are not in the language recognized by this PDA.

4. Give a CFG for the language recognized by this PDA.

2 Regular Language Machine vs CFL Machine

1. Explain two differences between the formal description of an DFA and the formal description of a PDA.

2. Two machines are considered equivalent if they recognize the same language (i.e., they accept the same strings).

   Come up with a function \texttt{convertD2P} : \texttt{DFA} \rightarrow \texttt{PDA} where, given an input DFA that satisfies the formal definition of DFAs from class, e.g., M = (Q,\Sigma,\delta,q_{start},F), \texttt{convertD2P} produces a PDA that satisfies the formal definition of PDAs, e.g., P = (Q_P,\Sigma,\Gamma,\delta_P,q_P,F_P), that is equivalent to the input DFA.

   To prove "equivalence" of two machines, use the typical "Examples Table", where the two columns being compared are the two machines.

3 A Regular Language is Context-Free

Every regular language is a context-free language!

Give three proofs of this statement, using each of the three representations of regular languages that we have studied: DFAs, NFAs, and regular expressions.

At least one of the proofs must use the \texttt{convertD2P} function from the Regular Language Machine vs CFL Machine Problem above. You may also use any other functions we have previously defined, or theorems we have proven (either in lecture, or from previous hws).

4 Whitespace Checking is Context-Free?

The A Context-Free Language? problem from Homework 5 showed a CFL can enforce some basic whitespace checking (for a programming language like Python). This problem will show that not all whitespace requirements can be expressed as a CFL.

Specifically, prove that the following language \mathit{WS}_2, which contains a subset of Python if statements, is not a CFL. Use a proof by contradiction using the Pumping Lemma for CFLs.

\mathit{WS}_2 = \left\{\sqcup^*\texttt{if:}\downarrow\sqcup^*\texttt{elif:}\downarrow\sqcup^*\texttt{else:}\mid\downarrow\textrm{ is newline; }\sqcup\textrm{ is space; spaces on each line match}\right\}

\Sigma = \left\{\texttt{if:},\texttt{elif:},\texttt{else:},\sqcup,\downarrow\right\} (in real-world grammars, terminal (i.e., alphabet) "symbols" can be, and often are, whole words)