Homework 1

Last updated: Thu, 4 Nov 2021 14:27:45 -0400

Out: Mon Sept 13, 00:00 EST Due: Sun Sept 19, 23:59 EST

This assignment explores deterministic finite automata (DFAs).

Homework Problems

1. DFA Formal Description (4 points)

2. Alternate "Run" Function for DFAs (4 points)

3. Create a DFA (5 + 5 = 10 points)

4. More Fun with Induction (5 points)

5. README (2 point)

Total: 25 points

Submitting

Submit your solution to this assignment in Gradescope hw1. Please assign each page to the correct problem.

A submission must include a README containing the required information, in addition to the solution to the problems. Please make sure your solutions are legible.

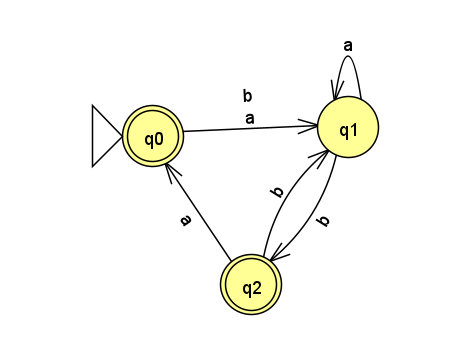
1 DFA Formal Description

Recall that a DFA’s formal description has five components, e.g. M = (Q,\Sigma,\delta,q_0,F).

Come up with a formal description for the following DFA:

2 Alternate "Run" Function for DFAs

Assume we have some DFA M = (Q,\Sigma,\delta,q_0,F).

In class, we defined a "run" function for DFAs, \hat{\delta}:Q\times\Sigma^*\rightarrow Q:

• \hat{\delta}(q,\epsilon) = q

• \hat{\delta}(q,wx) = \delta(\hat{\delta}(q,w),x)

Above, in the recursive case, x\in\Sigma, w\in\Sigma^*, and the single step transition function \delta is applied to a recursive call to \hat{\delta}, and the last character in the input

Define an equivalent, alternate "run" function called \hat{\delta_f}, which applies the one-step \delta function to the first character in the input instead of the last one. (Don’t forget to include the base case.)

3 Create a DFA

Prove that the following language is regular:

\{w\mid w\textrm{ has exactly two }\texttt{1}\textrm{s}\}

Assume the language contains strings from alphabet \Sigma=\{\texttt{0},\texttt{1}\}

4 More Fun with Induction

Prove that if some DFA M = (Q,\Sigma,\delta,q_0,F) has a state q such that \delta(q,a)=q, for all a\in\Sigma, then \hat{\delta}(q,w)=q for all possible strings w\in\Sigma^*. Use induction on the length of w.