▼CS622:   Theory of Formal Languages
►Homework 5
On this page:
1 Not a Context-Free Language
2 Turing Machine Config Sequences
3 Turing Machines and Closed Operations
4 Venn Diagram Correctness
    ← prev  up  next → 

Homework 5

Last updated: Thu, 4 Nov 2021 14:32:24 -0400

Out: Mon Oct 18, 00:00 EST Due: Sun Oct 24, 23:59 EST

This assignment starts to explore Turing Machines.

Homework Problems

  1. Not a Context-Free Language (6 points)

  2. Turing Machine Config Sequences (2 + 2 + 2 + 2 = 8 points)

  3. Turing Machines and Closed Operations (3 + 3 + 4 + 3 + 3 + 4 = 20 points)

  4. Venn Diagram Correctness (3 + 3 = 6 points)

  5. README (2 point)

Total: 42 points

Submitting

Submit your solution to this assignment in Gradescope hw5. Please assign each page to the correct problem.

A submission must include a README containing the required information, in addition to the solution to the problems.

1 Not a Context-Free Language

Prove that the language

L = \left\{ D\mid D\textrm{ is a string representing a valid DFA}\right\}

is not a context-free language.

In this language, a string representation of a DFA is exactly as defined by the formal definition, where tuples are enclosed in parentheses characters, sets are enclosed with brace, and each component is separated with a comma. The transition function is defined as a set of triples Q\times\Sigma\times Q. All the other components—the states, alphabet, start state, and accept states—are as we’ve seen before.

Here is an example string in L: (\{q_0,q_{accept}\},\{0\},\{(q_0,0,q_{accept}),(q_{accept},0,q_{accept})\},q_0,\{q_{accept}\})

This is a valid DFA because the start state and accept states are drawn from the set of states and every state has transitions for every possible character in the alphabet.

Here’s some invalid DFA descriptions:

  • (\{q_0,q_{accept}\},\{0\},\emptyset,q_0,\{q_{accept}\})

    This is invalid because it does not have transitions for some characters in some states.

  • (\emptyset,\{0\},\{(q_0,0,q_{accept}),(q_{accept},0,q_{accept})\},q_0,\{q_{accept}\})

    This is invalid because the transitions refer to states that are not in the set of states.

  • (q_0,\{0\},\{(q_0,0,q_{accept}),(q_{accept},0,q_{accept})\},q_0,\{q_{accept}\})

    This is an invalid DFA because the set of states is not a set.

  • 12345678910

    This is an invalid DFA because it does not have any of the required components.

2 Turing Machine Config Sequences

Here is the example Turing Machine from class (it’s also Figure 3.10 in Sipser textbook):

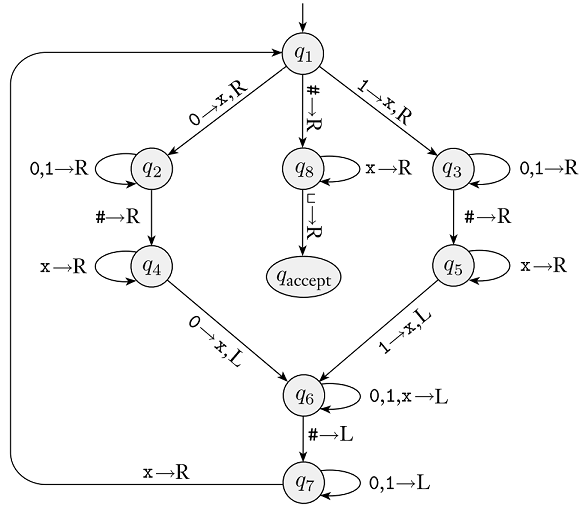
Remember that transitions for any input characters that are not explicitly included goes to an implicit q_{reject} state. Also, if a transition does not specify a character to write, then the tape contents stay the same.

Using this machine, give the sequence of configurations for the following input strings:

  1. 0

  2. 0##0

  3. 01#01

  4. 11#10

3 Turing Machines and Closed Operations

Show that Turing-decidable languages are closed under the following operations:

  • union

  • concatenation

  • complement

    Additionally, explain why your solution for showing that complement is closed for decidable languages won’t work for showing that complement is closed for recognizable languages.

    Hint: The complement of a set is the set of all elements not in the set.

Show that Turing-recognizable languages are closed under the following operations:

  • union

  • concatenation

  • The Decode Operation

    Additionally, explain why your solution for showing that DECODE is closed for recognizable languages won’t work for showing that DECODE is closed for decidable languages.

Each answer should be a short informal description of a Turing Machine, but remember that informal does not mean imprecise or incomplete. Answers must still be sufficiently precise so someone could reconstruct a formal machine if needed.

In particular, make sure to be careful with non-termination (when appropriate), and include a termination argument (when necessary)!

4 Venn Diagram Correctness

We’ve seen this Venn diagram in class many times:

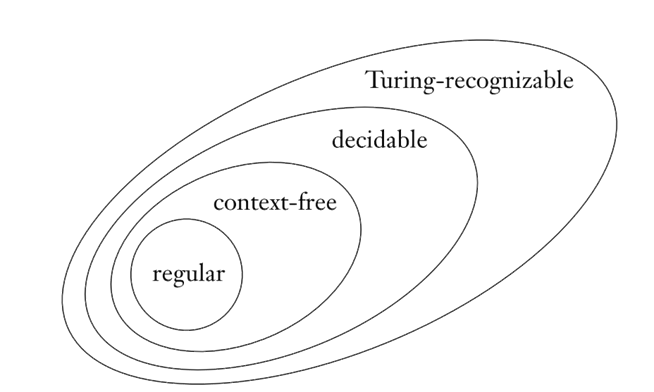
But it is actually correct?

In Homework 4’s NFA->PDA problem, you proved correctness of one part of the diagram, by showing that every regular language is also context-free. Thus the oval for regular languages should be completely inside (i.e., it’s a subset of) the oval for context-free languages.

Now prove that the rest of the diagram is correct. Specifically:

  1. Show that it’s correct for the "context-free" oval to be completely inside the "decidable" one.

  2. Do the same thing for the "decidable" and "recognizable" ovals.

Make sure your answer is clear about any statement(s) being proved, assumptions, and previous theorems or definitions that are being used. Also, don’t forget a termination argument if it’s needed.

HINT: Are there previous theorems from our "library" that can help?

    ← prev  up  next →