Homework 2

Last updated: Wed, 9 Feb 2022 20:09:28 -0500

Out: Mon Feb 07, 00:00 EST Due: Sun Feb 13, 23:59 EST

This assignment explores nondeterministic finite automata (NFAs).

Homework Problems

1. NFA Formal Description (5 + 5 = 10 points)

2. Exending the definition of "REACHABLE" (5 points)

3. DFA->NFA (5 points)

4. Another Closed Operation on Regular Language (5 points)

5. README (1 point)

Total: 26 points

Submitting

Submit your solution to this assignment in Gradescope hw2. Please assign each page to the correct problem and make sure your solutions are legible.

A submission must also include a README containing the required information.

1 NFA Formal Description

1. Recall that a NFA’s formal description has five components, e.g. N = (Q,\Sigma,\delta,q_0,F), where \delta:Q\times\Sigma_\varepsilon\rightarrow\mathcal{P}(Q) is the transition function mapping a state and input symbol (or no symbol, in the case of an empty transition) to a set of states.

   Come up with a formal description for the following NFA:

   

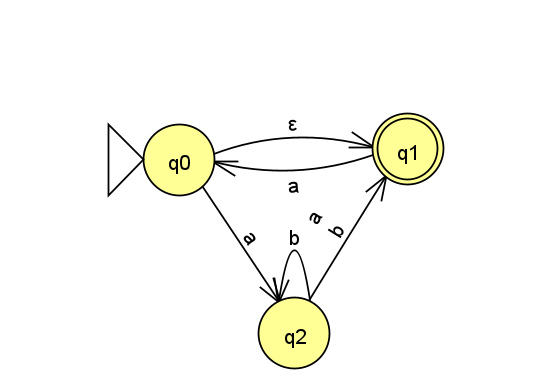
2. Come up with the result of the following computations and say whether it represents an accepting computation:

   1. \hat{\delta}(q0,\varepsilon)

   2. \hat{\delta}(q0,\texttt{a})

   3. \hat{\delta}(q1,\texttt{ba})

   4. \hat{\delta}(q2,\texttt{abb})

   5. \hat{\delta}(q0,\texttt{abb})

2 Exending the definition of "REACHABLE"

Define \varepsilon\textrm{-{\footnotesize REACHABLE}}_{qs}, which is like the \varepsilon\textrm{-{\footnotesize REACHABLE}} definition from class, except its input is a set of states.

Hint 1: You are allowed to call the \varepsilon\textrm{-{\footnotesize REACHABLE}} for single states that we defined in class in your definition of \varepsilon\textrm{-{\footnotesize REACHABLE}}_{qs}.

Hint 2: The definition of \varepsilon\textrm{-{\footnotesize REACHABLE}}_{qs} is very straightforward. In particular, it does not need to be a recursive definition.

3 DFA->NFA

In class we showed how to convert an NFA into an an equivalent DFA. Now show how to do the opposite: convert a DFA to an equivalent NFA.

More specifically, come up with a procedure \texttt{DFA}\!\!\rightarrow\!\!\texttt{NFA} that converts DFAs to equivalent NFAs. In other words, given some DFA M = (Q,\Sigma,\delta,q_0,F) that satisfies the formal definition of DFAs from class, \texttt{DFA}\!\!\rightarrow\!\!\texttt{NFA}(M) should produce some NFA N = (Q^\prime,\Sigma,\delta^\prime,q^\prime_0,F^\prime) that satisfies the formal definition of NFAs and accepts the same language as M.

4 Another Closed Operation on Regular Language

Define the following operation, called \mathrm{SUB}, on languages:

\mathrm{SUB}(A,B)=\{w\mid w\in A\textrm{ and }w \notin B\}

Prove that \mathrm{SUB} is closed for regular languages.