Homework 5

Last updated: Mon, 28 Feb 2022 00:08:09 -0500

Out: Mon Feb 28, 00:00 EST Due: Sun Mar 06, 23:59 EST

This assignment continues exploring context-free languages, with pushdown automata.

Homework Problems

1. A Pushdown Automata Example (6 + 4 = 10 points)

2. Design Your Own PDA (8 points)

3. CFLs Can Have Closed Operations Too (3 + 3 + 3 = 9 points)

4. NFA->PDA (8 points)

5. README (1 point)

Total: 36 points

Submitting

Submit your solution to this assignment in Gradescope hw5. Please assign each page to the correct problem and make sure your solutions are legible.

A submission must also include a README containing the required information.

1 A Pushdown Automata Example

For the following PDA state diagram:

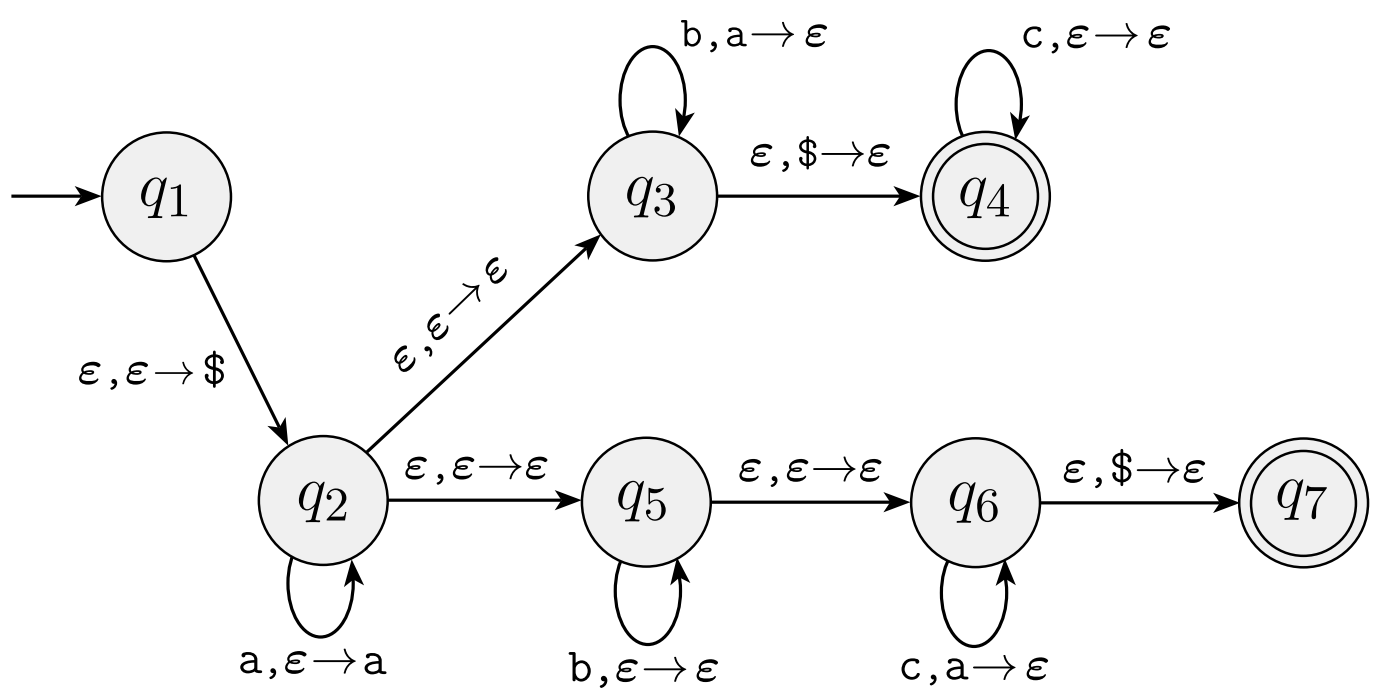
1. Give a complete formal description for this PDA,

2. and then give one possible computation sequence, i.e., a sequence of PDA configurations, for each of following input strings. If the computation does not end in an accept state, briefly explain why it gets stuck.

   1. \texttt{aabbc}

   2. \texttt{abbccc}

2 Design Your Own PDA

Come up with a PDA for the language from the Design a CFG problem in Homework 4:

L = \left\{w\mid w = \mathrm{rev}(w)\right\}

(where \mathrm{rev} is the function you defined in Reversing Strings from Homework 3)

You can assume alphabet \Sigma = \{\texttt{x},\texttt{y}\}.

Submitting just a state diagram for this problem is acceptable.

3 CFLs Can Have Closed Operations Too

4 NFA->PDA

Come up with a conversion function \texttt{NFA}\!\rightarrow\!\texttt{PDA} that, given some NFA N = (Q_N,\Sigma,\delta_N,q_N,F_N), produces an equivalent P = (Q_P,\Sigma,\Gamma,\delta_P,q_P,F_P).

This also proves that every regular language is also a CFL! (Note: the opposite is not true)