▼CS420:   Intro to Theory of Computation
►Homework 6
On this page:
1 Not a Context-Free Language
2 Turing Machine Config Sequences
3 Flashback:   Closed Operations for Regular Languages
4 Closed Operations on Turing-Recognizable Languages
    ← prev  up  next → 

Homework 6

Last updated: Fri, 11 Mar 2022 18:36:52 -0500

Out: Mon Mar 07, 00:00 EST Due: Sun Mar 20, 23:59 EST (Note: after Spring Break)

This assignment begins to explore Turing Machines and their languages.

Homework Problems

  1. Not a Context-Free Language (8 points)

  2. Turing Machine Config Sequences (6 points)

  3. Flashback: Closed Operations for Regular Languages (5 + 5 = 10 points)

  4. Closed Operations on Turing-Recognizable Languages (5 + 5 = 10 points)

  5. README (1 point)

Total: 35 points

Submitting

Submit your solution to this assignment in Gradescope hw6. Please assign each page to the correct problem and make sure your solutions are legible.

A submission must also include a README containing the required information.

1 Not a Context-Free Language

Prove that the following language of "states":

D = \left\{ q_1\texttt{\#}\cdots\texttt{\#}q_n\texttt{\#}q_0 \mid n\geq 1\textrm{, each }q_i\textrm{ is a string of len}> 0\textrm{, and }q_0 = q_j\textrm{ for some }j\geq 1\right\}

is not a context-free language.

You may assume the alphabet of the language is \Sigma = \{\texttt{\#},\texttt{a},\texttt{b},\texttt{c}\}, but that state name strings only use characters in \{\texttt{a},\texttt{b},\texttt{c}\}.

Here are some example strings in D:

  • \texttt{a\#b\#a}

  • \texttt{aa\#bb\#bb}

  • \texttt{aa\#aa}

Here are some example strings not in D:

  • \texttt{a}

  • \texttt{aa\#\#bb}

  • \texttt{a\#b\#c}

2 Turing Machine Config Sequences

Here is the example Turing Machine from class (it’s also Figure 3.10 in Sipser textbook):

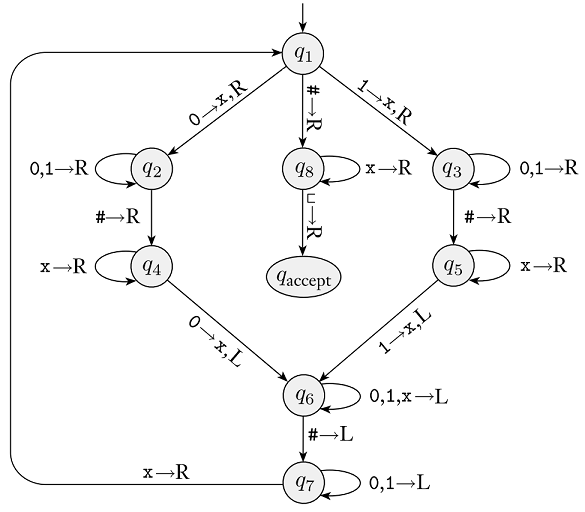
Remember that transitions for any input characters that are not explicitly included goes to an implicit q_{reject} state. Also, if a transition does not specify a character to write, then the tape contents stay the same.

Using this machine, give the sequence of configurations for the following input strings (you must use the textual representation of a configuration):

  1. 0#0

  2. 10#10

  3. 10

  4. ##11

3 Flashback: Closed Operations for Regular Languages

  1. Define the following operation, called \mathrm{NOTIN}, on languages:

    \mathrm{NOTIN}(A)=\{w\mid w \notin A\}

    Prove that \mathrm{NOTIN} is closed for regular languages.

  2. Define the following operation, called \mathrm{BOTH}, on languages:

    \mathrm{BOTH}(A,B)=\{w\mid w \in A\textrm{ and }w \in B\}

    Prove that \mathrm{BOTH} is closed for regular languages.

4 Closed Operations on Turing-Recognizable Languages

  1. Prove that the \mathrm{BOTH} operation (from the Flashback: Closed Operations for Regular Languages problem) is closed for Turing-recognizable languages.

    To further show that your answer is correct, create a table of possible Turing machine outcomes, like the ones from lecture, that show all possible combinations of results from all of the Turing machines involved in your answer.

  2. Create a table of possible Turing machine outcomes, like the ones from lecture, that show what a hypothetical Turing machine would need to do in order to prove that the \mathrm{NOTIN} operation (from problem Flashback: Closed Operations for Regular Languages) is closed for Turing-recognizable languages.

    Then comment on why it might not be possible to prove that the \mathrm{NOTIN} operation is closed for Turing-recognizable languages.

    ← prev  up  next →